The 2 problems that we solve
We have one answer, that can handle two questions:
- CashFlow Forecast
- Investment Evaluation (calculation of the profitability of a proposed investment)





CashFlow Forecast
We need to determine the need for future working capital, establish future Bank loan balances, and calculate “Interest Expense” and “Interest Income”. Examples are:
- Let’s say that we are in Feb 2024, and we want to see how our Bank balance will look like, from Feb 2024 until Dec 2024 (a horizon of today plus 10 months)
- We are in Sep 2024, and we are working on the Annual Budget of 2025. We want to see how our Bank balance will look like, from Sep 2024 until Dec 2025 (a horizon of today plus 15 months). The problem is more complicated, not because we have more months, but because we have a new Fiscal Year, and so, we must calculate several year-end values for FY 2024, like “Dividends Payable”, “Income Tax Payable”, “Advance Payment for Income Tax of Next FY” etc.
Investment Evaluation (calculation of the profitability of a proposed investment)
We evaluate the possibility to
- create a new company from scratch.
- in an existing company, to add a new sales location.
- in an existing company, to add a new factory.
- in an existing factory, to add a new production line.
- in an existing production line, to add a new product.
- etc.
Plus, there are other questions that are associated with that problem (Break-Even point, Sensitivity Analysis, What-if scenarios etc.).
What we must do, before the calculation
In both scenarios, we begin with the collection of values, that are expected to happen. Let’s call them “Forecasted Values“. Examples are:
- Sales
- Salaries
- Ads
- Travel Expenses
- Rent
- Interest Rates
- FX Rates
- Etc.
On their basis, we must calculate other values, that are dependent on them. Let’s call them “Calculated Values“. Those should NEVER be treated as a “matter of forecast”, but only as a “product of calculation”. Examples are:
- Interest Expense
- Interest Income
- Purchases of merchandise, raw materials, packaging materials etc.
- Direct labour expenses
- Payment of VAT
- Payment of Income Tax, and advance payment for next year’s Income Tax
- Payment of Dividends
- Almost all kinds of Taxes
- Etc.
The previous “State-of-the-Art” in calculation methods
Fact 1:
If we go to 100 companies, and ask to see how 100 different CFOs (in other words, experienced high level professionals, with MBA’s or Master’s in Finance, or PhD’s), we will receive 100 different spreadsheets, that implement 100 different calculation methods, that arrive at 100 different results, for the same problem, with the same list of assumptions.
Fact 2:
If we go to Wikipedia (with over 6.8 mil English articles), and search for an article, that lists the steps of a calculation method to solve those two problems, we will see that there is no such article. Instead, there are a handful of small articles, that describe some vague and high-level guidelines. But even as such, if you look closely, half of their contents cannot stand up to scrutiny. And a few of those vague and high-level guidelines, cannot even pass the laugh test.
From the above facts, it is easy to deduce that, currently, the biggest problem with the “State-of-the-Art”, is that:
There is no “State-of-the-Art”
Or, in other words, there is no commonly accepted calculation method, for Finance professionals to use and implement.
Who is to be blamed for that?
This whole situation, reminds of what took place 150 years ago in Medicine, when there were no antibiotics. Patients visited their doctors, in hopes of getting well, but instead, they died.
Were doctors to be blamed for that high mortality rate? No. The blame rested with the “State-of-the-Art”, which had not provided the appropriate tool (antibiotics) to the professionals of the field.
Today, Finance professionals need the appropriate tool to do their job. They need a Commonly Accepted Calculation Method, whose result can stand up to scrutiny and verification.
What is being implemented by others
Even though the number of problems and inaccuracies, in the way that Finance professionals are approaching those two problems, are legion, at the end of the day, those two tasks must be done. Someone, somehow, must produce some kind of result.
What is being implemented (thru spreadsheet), is a list (a.k.a. the “single ledger entry“ method). For more on that, please read the following article in our blog.
What Finance professionals need

When we say that “Forecasted Sales = 10 mil USD”, we know that the actual final sales figure, is not going to be “exactly 10 mil USD”. The forecasting process (by definition) has a built-in inaccuracy. Generally speaking, let’s call it a ±Α% built-in inaccuracy.
If the calculation method has built-in inaccuracies (and the current spreadsheet-implemented way of working, has many – let’s call it a ±B% inaccuracy), we end up with a result whose inaccuracy is ±(Α*B)% .
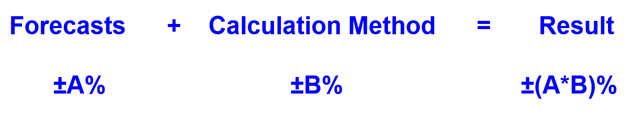
What we need, is a calculation method, who’s inaccuracy is ZERO (B=0).
Actually, such a calculation method, has existed for many centuries. However, its implementation in forecast mode (until yesterday) was neither easy, nor practical or feasible.
In University, we were taught that method, under the name “Accounting 101″. Everyone will agree that “Sales” means that we Debit this account, and we Credit that account. That is a common language that we all know/use, and we accept it as accurate and trustworthy.
At a first casual glance, one might be tempted to think that, since “Accounting 101” is so successfully being implemented, thru the numerous ERPs that exist, it would be a good idea to use one of them, in order to create the company’s future Accounting Books. Just try it, and in five minutes (or less) you will discover that (on a practical level) ERPs cannot work in forecast mode, because there are too many calculation incompatibilities, between processing actual data, versus processing forecasted data. For more on that, please read the following article in our blog.
What is the C2BII approach and calculation method
We are creating an automated simulation of the company’s future Accounting Books. As a starting point, most of the things that you will be required to perform, are based on the Accounting know-how, that you already have and use (Accounting 101 – Assets and Liabilities – Debit and Credit).
The theory might sound simple. However, the implementation will need a secret sauce that will make it look and feel easy and practical. That can be found in our US Patents.
For a first taste of the new calculation method, and the software tool that implements it, please first read the articles in the blog.
Then, please contact us for a demo.